The heart and soul of elliptic, flat (Euclidean), and hyperbolic spaces

... is constant, polynomial, and exponential.

Think about building cellphone towers in a Euclidean plane. First, we choose the central station arbitrarily at point $O$, and call it the "origin". To cover all space that's within a distance $R$ to the origin, we need $O(R^2)$ stations.

This is polynomial growth.

Then think about building cellphone towers on a spherical surface, on a little asteroid. Then it's clear that there's only a constant number of towers needed no matter how big $R$ is chosen, since the whole surface has finite area. So we need $O(1)$ stations.

This is constant "growth".

Then, if you know how to play in hyperbolic space (if not, go play Hyperrogue!), you'd know that the number of stations grows as $O(\exp{(CR)})$, where $C=(-K)^{-1/2}$, and $K$ is the Gaussian curvature of the plane. This can be derived by using the formula of the area of a hyperbolic circle of radius $R$:
$$\frac{4\pi}{-K} \sinh^2 \frac{r}{2\sqrt{-K}} $$

We normalize $K = -1$ to get the growth rate $O(\exp{R})$.


The heart of flatness is polynomial. The heart of ellipticity is constant. The heart of hyperbolicity is exponential.

An autopsy of Greek-style Geometry

The history is well-known. I'll just sketch. In Ancient Egypt, they used geometry for building and measuring land. In Ancient Babylon, they did a lot of astronomy, but geometry wasn't that important to them, as their astronomy were mostly about counting the number of days until Venus is visible at dawn again, things like that. For that, they mostly used arithmetic series.

In Ancient Greece, there were a lot of axiomatic geometry, as you know from the very name "Euclid". They also did a lot of practical geometry and astronomical geometry.

Even though spherical geometry is rather obscure in modern times, in the past, it was very popular. Ocean sailing needs it, and astronomy needs it, two big consumers of geometric knowledge. Spherical geometry actually was just as advanced as flat geometry back then.

In fact, the first trigonometric table was a table of chords made by Hipparchus for the use of astronomy. And On the Moving Sphere (4th century B.C.) is believed to be the oldest mathematical treatise from ancient Greece that is completely preserved.

Chord table of Ptolemy. It's all Greek to me, literally.

We then skip over a thousand years to about 18th century, when hyperbolic geometry finally got discovered. This history has been presented many times, so you can just search "discovery of hyperbolic geometry" and watch.

By the beginning of the 20th century, Greek-style geometry (aka high school geometry), where you can draw pictures and reason about it with axioms and propositions, has reached its completion. Hilbert and others like him published very rigorous books about it, proving everything perfectly.

There will be no more breakthroughs in Greek-style geometry, just like there will be no more breakthroughs in Newtonian physics, or special relativity -- it has been studied to death.

Geometry turns floppy: centipede mathematics gone wild

Geometry, which used to mean things that are so rigid, you can draw them with rulers and compasses, and build a pyramid that can stand a thousand years using it, grew bigger, to include the soft (topological), the dotty (discrete), and the higher-dimensional.

The main thing is that since the 20th century, mathematics has become extremely abstract. There's a nice phrase "centipede mathematics":

The term is attributed to Polish mathematician Antoni Zygmund. Zygmund is said to have described the metaphor of the centipede thus: "You take a centipede and pull off ninety-nine of its legs and see what it can do.". Thus, Zygmund has been known by many mathematicians as the "Centipede Surgeon".

For more on centipede mathematics, see the nLab entry.

When this philosophy is applied to geometry, we get lots and lots of new "geometries", things like projective geometry over the complex numbers, geometric topology (think about Klein bottles knotted in 4-dimensional space), Riemannian geometry, Hilbert space geometry ("infinite dimensional geometry")...

Basically, as long as you can use pictorial reasoning to study it, it's geometry!

With geometry made fluid, hyperbolic geometry extended to more than just pictures in a plane. People started studying hyperbolic manifolds, hyperbolic groups, hyperbolic metric spaces, hyperbolic dynamics, etc. The key idea is still exponential growth of some kind of area, in relation to some kind of distance.

In hyperbolic manifold, the theory is still very close to the original hyperbolic geometry. Basically, instead of having constant negative curvature on an infinite space that looks the same everywhere, we consider a manifold with negative/nonpositive curvature locally everywhere. Locally, there's no difference from classical hyperbolic geometry, it's only when you go global that things start becoming different.

In hyperbolic group theory, we attempt to make a group into a geometric space by imposing the word metric on it. Some groups look like a hyperbolic plane when viewed as a metric space this way. Basically, you can get exponentially many different elements in the group via appending only a few letters. For example, $F_2$, the free group on two elements is such a group. It's no coincidence that the Cayley graph of $F_2$ is best drawn on a hyperbolic plane.

In hyperbolic metric space, the nearness of points compared to the bigness of area is abstractly formulated using geodesic triangles. Basically, a triangle is $\delta$-thin iff any point on one edge is within distance $\delta$ of its other two edges. A space is $\delta$-hyperbolic iff all its triangles are $\delta$-thin.

Hyperbolic dynamics: one way to get butterfly effect

Dynamical system studies how a system changes in a geometric style. Imagine the world to be a little speck of dust floating in its phase space, and its trajectory determined purely by a field of wind in the space... thus is the world in the eye of a perfect scientist.

We are imperfect scientists, so we imagine the world to be a cloud of dusts, the cloud representing our uncertainty to the exact state of the world. Then watch the cloud flow and distort. 

The study of the shape of a dust cloud in a wind field is the heart and soul of dynamical system theory. Does the cloud keep itself together, as it must be in a parallel wind field? Then the world is very predictable, and our uncertainty never grows. We can watch the world once, close our eyes, and never open again, and forever able to predict with good accuracy. Does the cloud spread out thinly into a mist around the whole phase space? Then we cannot predict far into the future, and in fact cannot predict with any certainty other than "in the far future, the world would look like a generic world picked at random from the whole phase space".

As a side note, ergodic theory studies ergodicity, one way for ergodicity to happen is for almost all world-trajectories to visit the whole phase space. This is one way to get butterfly effect.

If the wind field is stable, there cannot be any accumulation of air, so the wind field should keep the volume of any dust cloud constant (so the wind flow is a "measure-preserving map"). 

How to spread the dust cloud around without changing its volume? We can't spread it around like a mist, but we can do something close to it: shear the cloud long and thin, then wind it around the space like a cotton candy:

So we have two problems: elongating the cloud; winding it around the space densely.

Step 1: elongating

Step 2: cotton-candying

Hyperbolicity is a technique for elongating the cloud. Basically, just push it in one direction and pull in another:

The cotton-candying of the cloud comes later, but turns out that, for reasons I don't yet fully understand, hyperbolicity usually gives cotton-candying as a bonus!

Homoclinic tangle: taffy cotton candy

The center of that wind field drawn above is a place of calm. If you sit there, you'll be fixed there forever. It's what is called a "hyperbolic fixed point" or "saddle point". 

If you draw the downhill directions, you get the same wind field, with the saddle point being the hyperbolic fixed point.

But if you are sitting just a bit away from it, you'll be moved. 

Every point on the x-axis gets carried towards the fixed point, so the x-axis is called the "stable manifold" of the fixed point. The reverse is true for the y-axis, so that's called the "unstable manifold". Clearly, they are symmetric: if you reverse the wind directions, the hyperbolic fixed points remain, but their stable and unstable manifolds are switched.

If you know manifold theory, you can look up the Stable Manifold Theorem, which says that if the wind field is $C^k$, then the stable and unstable "manifolds" are $C^k$-manifolds that are tangent to the contracting and expanding subspaces at the fixed points.

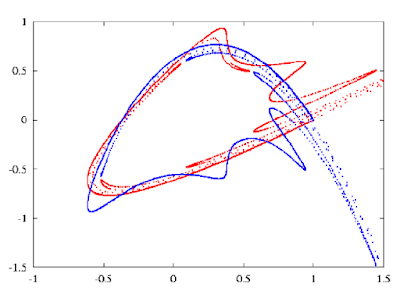
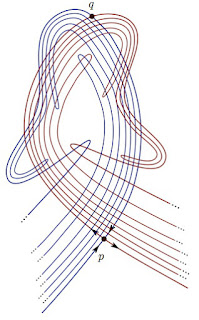
 Consider a wind field with one hyperbolic point $p$, and draw out its stable and unstable manifolds. If there exists a point $q$ where they intersect (such points are called "homoclinic points"). Then, by some reasoning I'm not quite understanding, this intersection would make the two manifolds go crazy and start tangling up into a "homoclinic tangle"

I'll just put up more pictures of the tangle, since I can't explain more. Where words fail, math speaks.

From Chaos and its manifestations

From Homoclinic tangle of the ideal separatrix in the DIII-D tokamak from (30,10)+(40,10) perturbation (2014)

From here.

From chapter 4 of this

I don't have much to say but to moan in pleasure at the sight of such beautiful tangles. These sublime cotton candies, more delicate than a morning gossamer, but more unbreakable than the red strings of fate, are the hoofprint of Celestia.

I would like to modestly append two pictures of my own production, obtained for a physics class project, concerning the dynamics of a double pendulum. They are plots for the time until a pendulum flips, with the x and y axes being the starting angles of the pendulums. From green to purple, the flipping time increases.

Flipping time of the lower pendulum.

Flipping time of the upper pendulum.

Why care?

Hyperbolic dynamical systems have a history stretching to Henri Poincaré's attempt to solve the three-body problem. This is well-documented and you can find the history easily online. 

Briefly, consider 3 bodies in space interacting by gravity. To completely specify the system, it's enough to know the positions and velocities of the bodies. Thus we have 6 vectors, 18 degrees of freedom. So the phase space of the system has 18 dimensions, and the problem is to study the curve that the system traces out in the phase space as it's blown about by the 18-dimensional winds.

Poincaré attempted to qualitatively picture the curves, and found a messy beast:

When we try to represent the figure formed by these two curves and their intersections in a finite number, each of which corresponds to a doubly asymptotic solution, these intersections form a type of trellis, tissue, or grid with infinitely serrated mesh. Neither of these two curves must ever cut across itself again, but it must bend back upon itself in a very complex manner in order to cut across all of the meshes in the grid an infinite number of times. The complexity of this figure will be striking, and I shall not even try to draw it.

From Scholarpedia, Hyperbolic dynamics (2008):

The theory of hyperbolic dynamical systems provides a rigorous mathematical foundation for... deterministic chaos - the appearance of chaotic motions in purely deterministic dynamical systems. The cause for these motions is the instability of trajectories that is expressed in terms of the hyperbolicity conditions... This hyperbolicity theory has many applications within mathematics, such as to geometry (geodesic and frame flows, theory of foliations), modern rigidity theory, dimension theory (multifractal analysis of dynamical systems) and statistical and mathematical physics.

Hyperbolic graphs: exponential number of friends

Trees in hyperbolic space

The usual way of drawing a binary tree quickly runs out of space, but you can draw it in hyperbolic space no problem: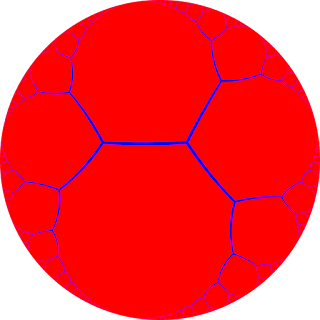

The order-3 apeirogonal tiling

The key to hyperbolic tree drawing is the fact that, a binary tree (and in general, any tree whose nodes have a roughly constant number of neighbors) has exponential growth: the number of nodes reachable within $n$ edges grows like $O(d^n)$, where $d$ is the usual degree of nodes. This exponential growth requires exponential space... thus, hyperbolic space.

Cayley graph of the free group on two elements.

Small world in biology and sociology

Remember "small world" or "six degrees of separation"? This surprising phenomenon has two key components that sounds contradictory:

1. The world is big. That is, there are a lot of people.
2. The world is small. That is, it's easy to reach almost anyone by a few personal relationships.

If we translate that into geometry, we have:

1. There are a lot of points. Exponential number of them, even.
2. But the distance between any two points is small.

If we try to embed these points into a space, giving each point some space (so that they aren't squashed together), we are forced to do it in a hyperbolic space.

Some social and biological networks have been shown to be hyperbolic, for good reasons. From Topological implications of negative curvature for biological and social networks (2014):

... a variety of biological and social networks are hyperbolic. This hyperbolicity property has strong implications on the higher-order connectivity and other topological properties of these networks. Specifically, we derive and prove bounds on the distance among shortest or approximately shortest paths in hyperbolic networks. We describe two implications of these bounds to crosstalk in biological networks, and to the existence of central, influential neighborhoods in both biological and social networks.

Another overview is Hyperbolic geometry of complex networks (2010).

Graph-drawing 

Examples of practical use of hyperbolic graph-drawing can be found here (HyperE: Hyperbolic Embeddings for Entities) and here and here and here.

Optimization-based construction

Combinatorial construction

Designed hyperbolic network

The hyperbolic graph of personal relationships spreads rumors fast. Inspired by this, perhaps such a network is good for sharing information quickly. This is suggested by Sustaining the Internet with hyperbolic mapping (2010).

In this paper, we present a method to map the Internet to a hyperbolic space. Guided by a constructed map, which we release with this paper, Internet routing exhibits scaling properties that are theoretically close to the best possible, thus resolving serious scaling limitations that the Internet faces today. Besides this immediate practical viability, our network mapping method can provide a different perspective on the community structure in complex networks.